Declinazione ( seconda parte )

Introduciamo adesso il concetto di sfera celeste, un'idea concepita per dare al cielo un valido sistema di coordinate, analogamente a quanto fatto con le coordinate terrestri.

Immaginando che la Terra sia al centro di una sfera vuota, che ha le stelle, le nebulose e le galassie dipinte sulla superficie interna della sfera ed il Sole, la luna ed i pianeti che si muovono, sempre sulla stessa superficie.

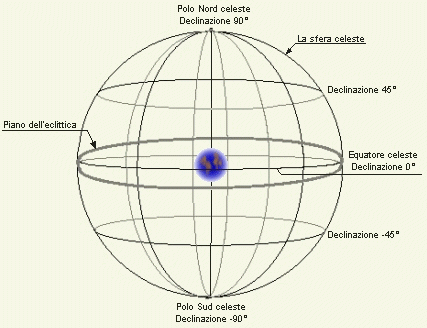
Proiettiamo le linee terrestri della latitudine e della longitudine sulla sfera e l'asse di rotazione terrestre che determinerà i poli celesti Nord e Sud. A questo punto, per determinare la posizione di un oggetto su questa sfera, basterà conoscere le relative coordinate che lo localizzano (naturalmente queste cambieranno velocemente per gli oggetti che si muovono rapidamente come i pianeti, e lentamente per quelli meno rapidi). Vedi anche precessione.

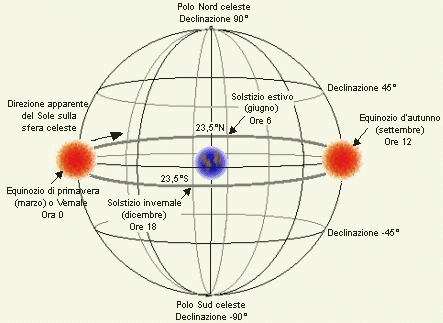
L'ascensione retta (A.R.) corrisponde alla longitudine celeste e, analogamente ad essa, è una distanza angolare, questa volta espressa in ore (h), minuti (m) e secondi (s) in un cerchio di 24 ore lungo l'equatore celeste, in direzione est a partire dal Punto vernale (o Primo punto d'ariete o Punto gamma). Poiché abbiamo bisogno di un punto di riferimento certo nella sfera celeste, non possiamo semplicemente proiettare il Meridiano Zero di Greenwich per avere un riferimento, quest'ultimo infatti, a causa della rotazione terrestre non sarebbe fisso. Al suo posto si utilizza invece il punto dove il Sole, nel suo moto apparente sulla sfera (cioé lungo l' eclittica), attraversa ogni anno l'equatore celeste da Sud verso Nord.

Ma perché si utilizzano le ore, i minuti ed i secondi anziché i gradi, come per la latitudine terrestre ? Perché è più conveniente utilizzare questa divisione che corrisponde al giorno siderale, il tempo necessario alla Terra, affinché compia una rotazione completa rispetto alla sfera celeste.

La declinazione (DEC), la latitudine celeste, è la distanza angolare, verso Nord o Sud, dall'equatore celeste misurata in gradi.

Puntando il telescopio (senza alcun motore guida), ad una coordinata, per esempio A.R.= 0 h, Dec=0°, e tornando dopo un'ora, potremo notare che il nostro strumento starà puntando all'A.R. = 1h, Dec = 0°. Poiché il moto di rivoluzione terrestre intorno al Sole contribuisce al moto apparente delle stelle, puntando il telescopio sempre al punto con A.R.= 0 h e Dec=0°, 24 ore dopo il telescopio punterà a A.R.= 0 h 4m, Dec=0° a causa della differenza tra giorno solare e giorno siderale. La conseguenza è che le stelle che stiamo osservando sembrano levarsi quattro minuti prima ogni giorno che passa.