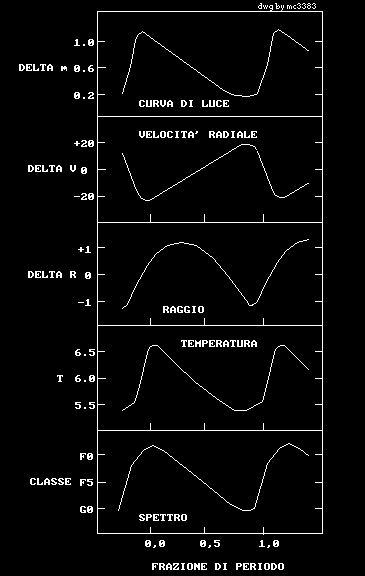
Queste stelle appartengono alla classe delle stelle pulsanti, cioè quelle stelle la cui variazione di luminosità è dovuta a pulsazioni radiali del raggio intorno ad una posizione media. La pulsazione di queste stelle è stata accertata grazie ad un grande numero di osservazioni e ad un intenso studio dei fenomeni da queste dedotti.

Elenchiamo brevemente questi fenomeni:
Solo ultimamente si è pervenuti ad una soluzione del problema grazie al progredire degli strumenti a disposizione degli astronomi, ma mentre prima si pensava ad un unico tipo di cefeidi, in seguito si comprese che ne esistono due tipi, ognuno con una propria relazione periodo-luminosità.Il primo tipo è costituito dalle cefeidi classiche (delta cephei o Cdelta) il secondo da stelle meno luminose, cioè dalle W virginis (CW), come si vede dalla figura:
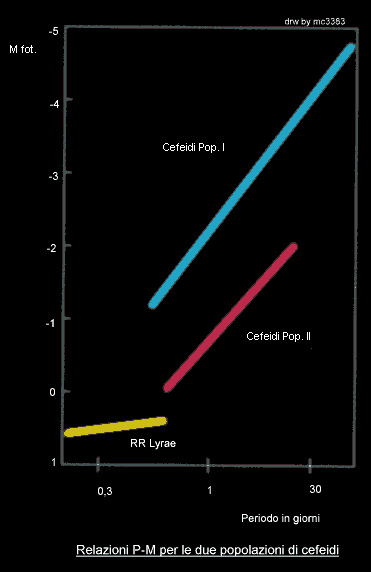
queste due relazioni sono praticamente parallele, ma le Cdelta sono sistematicamente più luminose di due magnitudini delle CW.
Inoltre è stato appurato che le Cdelta sono molto più giovani delle CW ed appartengono alla Popolazione I essendo state trovate negli ammassi. Le CW invece sono più vecchie ed appartengono alla Popolazione II, essendo state trovate nell'alone esterno della Galassia.
Immaginiamo una stella inizialmente in equilibrio idrostatico e comprimiamone la superficie. Al suo interno aumenterà la pressione, la temperatura e quindi il numero di reazioni nucleari. L'energia che si sprigiona, oltre all'aumentata pressione del gas, tenderà ad arrestare la compressione ed a far dilatare gli strati esterni, dilatazione che, per inerzia, proseguirà oltre la posizione di equilibrio. Dilatandosi la stella, diminuiranno le reazioni nucleari al suo interno, per cui ad un certo istante le forze gravitazionali prevarranno sulle forze di espansione e la dilatazione si arresterà, la stella tornerà a contrarsi ed inizierà un nuovo ciclo.
La stella quindi oscillerà periodicamente con un'ampiezza ed un periodo che dipendono dalle configurazioni geometriche e fisiche della stella. Questa pulsazione però, a causa degli inevitabili attriti interni, tenderà ad arrestarsi (come un oscillatore armonico smorzato), a meno che non esista un meccanismo che fornisca, per ogni ciclo, la spinta sufficiente a vincere gli attriti interni (proprio come un'altalena).
Già negli anni '20 S.A. Eddington, cercò di elaborare un sistema che descrivesse questo meccanismo, ma i progressi maggiori sono stati fatti da S.A. Zhevakin, J.P.Cox e R.F.Christy sviluppando innumerevoli modelli con l'aiuto del calcolatore. Il meccanismo è relativamente semplice e, come come giustamente intuito da Eddington, deve svilupparsi sotto gli strati superficiali delle stelle. Questo, similmente ad una valvola, impedisce l'uscita dell'energia nella fase di contrazione (quando aumenta la temperatura), per rilasciarla in fase di espansione, fornendo così la spinta necessaria a completare il ciclo. Se questo meccanismo è ben bilanciato, l'astro continuerà a pulsare per lunghissimo tempo.
Dalle misure osservative risulta che la parte (superficiale) della stella coinvolta nelle pulsazioni copre una regione di circa il 15% del raggio. Questi strati superficiali che partecipano alla pulsazione si possono dividere in tre parti:
Vediamo ora come è fatto questo meccanismo a valvola.Tre effetti contribuiscono ad eccitare la pulsazione:
Il meccanismo a valvola è dovuto alla somma di questi tre effetti. Lo strato di elio in cui ha luogo questo meccanismo, però deve essere ad una profondità ben stabilita; se si trovasse più in profondità, le pulsazioni (che hanno luogo nelle parti superficiali della stella) sarebbero smorzate in tale strato, per poter dare luogo all'effetto valvola.Viceversa se fosse troppo in superficie, la sua densità sarebbe così bassa da non consentire un'efficace oscillazione. Per cui se lo strato di elio deve avere determinate caratteristiche perchè abbia luogo la pulsazione, ne deriva che quest'ultima può avvenire soltanto in una particolare zona del diagramma H-R (la zona cioè dove l'astro possiede una determinata configurazione fisica).
Infatti se l'astro è troppo caldo, lo strato deve trovarsi troppo vicini alla superficie, se è troppo freddo, deve essere più in profondità. Questa zona del diagramma H-R dove ha luogo la pulsazione è detta fascia di instabilità delle Cefeidi, ed è stata determinata sviluppando al calcolatore vari modelli di queste stelle, basandosi su dati osservativi. Questa fascia, come si vede dalla figura
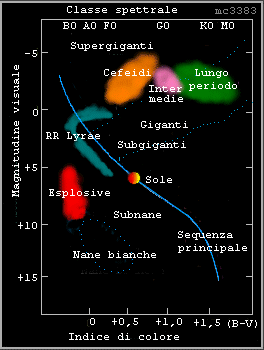
attraversa il diagramma H-R partendo dalla zona delle supergiganti, fino alla zona principale. Tutte le stelle che nel loro ciclo evolutivo attraversano questa fascia, sono costrette a pulsare, ipotesi questa, confermata dalle osservazioni.
Un fenomeno che si osserva durante la pulsazione è il phase lag o ritardo di fase. Si nota cioè che le variazioni di luminosità della stella sono in ritardo di circa 1/4 di periodo rispetto alla variazione del raggio:

Questo significa che la stella non è più luminosa quando è più grande e viceversa. Una spiegazione di questo fenomeno potrebbe essere che durante la pulsazione i vari strati della stella non sono rigidamente collegati tra loro. Così quando l'espansione cessa e la stella comincia a contrarsi, gli strati esterni proseguono nella loro corsa per inerzia, fermandosi in realtà solo quando la contrazione è già in stato avanzato. Per cui si crea un ritardo tra il massimo di luminosità ed il massimo delle dimensioni raggiunte dalla stella.